Can LLMs do math?

Large Language Models (LLMs) have caught the world by storm, performing many tasks in a superhuman speed and precision. Although these LLMs excel at Natural Language Processing (NLP) and understanding tasks, they fall behind when it comes to performing mathematics-related tasks. In this article we are going to find out why LLMs struggle with performing maths and common workarounds used to overcome these limitations.

Transformers 101 : Quick Sneak-Peek into Transformer architecture

Almost all SoTA LLMs have the infamous Transformer architecture in their core as the main prediction engine. So before we inspect why transformers lack maths skills, let’s see what we are dealing with. Here we see the ‘OG’ transformer model’s architecture that featured in the groundbreaking paper “Attention is all you need”. Although modern models have fewer architecture tweaks compared to this, we can get the overall idea by referencing this.

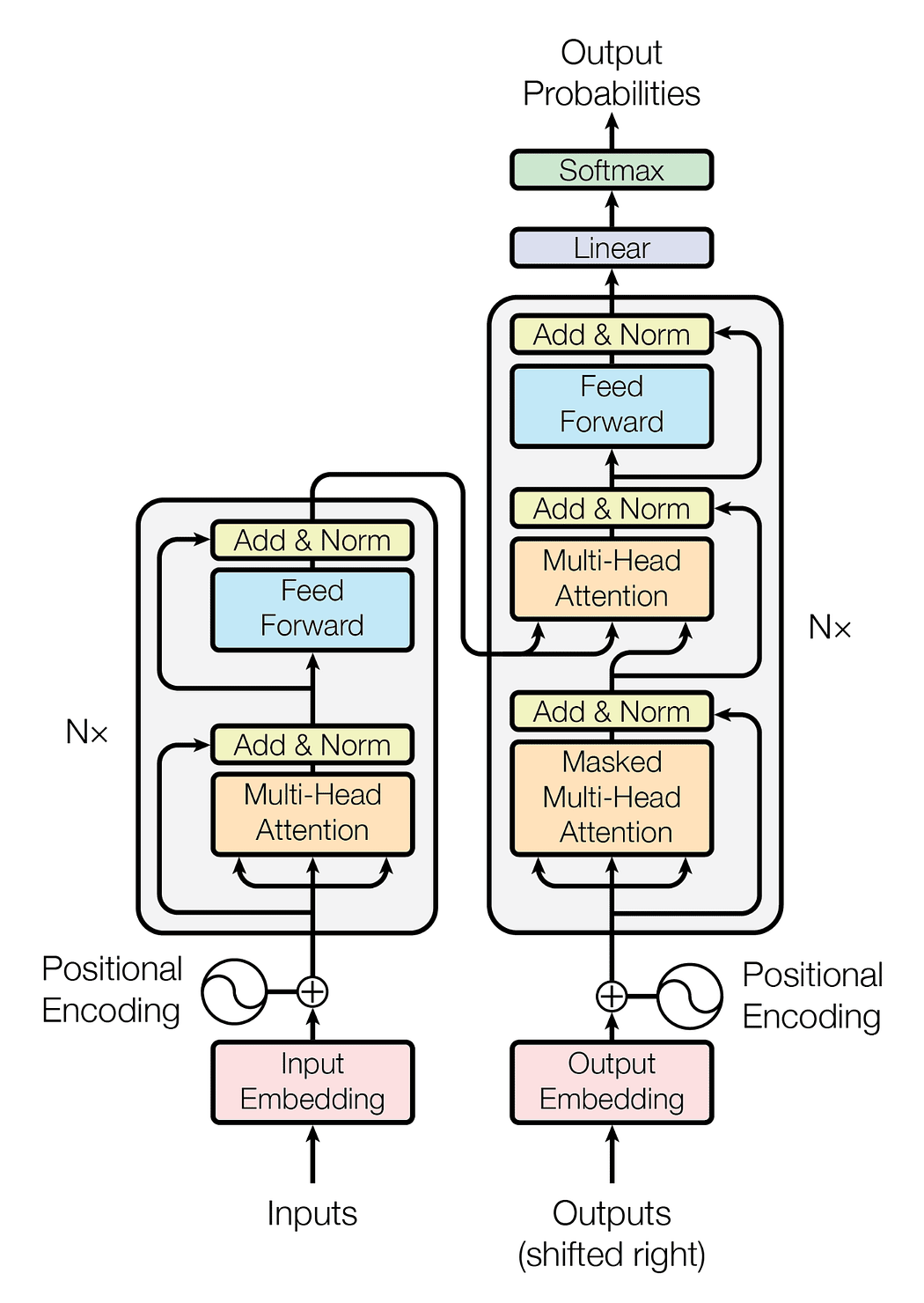
Vanilla Transformer Architecture (Reference :https://arxiv.org/abs/1706.03762)

Basically Transformer model contains 9 components and following are their description and main purpose of them

When a LLM is trained it undergoes 3 main training phases:

• Pre-training: Here, self-supervised learning is used to train the model to predict the next token given an input sequence of tokens. A vast amount of text data is used here to give as much information to the model. Basically the model learns syntax, grammar and factual knowledge from the input text here.
• Supervised fine-tuning: After pre-training, the model’s weights are fine-tuned on task-specific dataset. As an example, if the model is expected to be a chat-based model, then the model is fine-tuned with a curated Q&A dataset to improve the question-answering ability.
• RLHF: Reinforcement Learning or Reinforcement Learning with Human Feedback are used to align the model’s responses with human preferences. Initially the model’s responses are ranked by humans and using that data a reward model is trained. Then RL is used to update the model using policy optimization techniques such as Proximal Policy Optimization (PPO).

Why LLMs are not that good at maths

Now that we have a good understanding about what's under the hood in an LLM, let’s briefly see why LLMs lack maths skills .

• Transformers are not calculator: As we learned in the previous chapter, LLMs are trained to predict the next word and are fine-tuned to predict words based on human preferences. Also LLMs don’t have any compute engines like the ALUs that we see in computers. So when a math question is given, they technically process it as a sequence of tokens and try to predict the next token. Instead of doing arithmetic operations, the model tries to predict the tokens based on patterns learned in the trained data, which might have included some examples related to the input. For example, GPT-3 could perform arithmetic operations on small numbers because it probably saw enough examples and learned some patterns from them in the training data. But when it comes to large numbers, it often gets the first few digits right and starts to make errors in the rest of the numbers (I.King). This behaviour confirms that the model doesn't exactly perform the correct algorithm, but approximates the answer based on its training data

• Encoding complications: As we saw in the architecture of transformers, any input that is given to the transformer model is processed as tokens (Ex: Subwords). So when numerical inputs are given to an LLM , it breaks the whole number into sub tokens which contains partitions of the input numbers (Ex: the 123456.45 number will be split in to tokens “123” , “456” , “.45”). So this tokenization adds bias and systematic errors while learning the patterns from the data. Recently it was discovered that models like GPT3.5 and GPT4 show stereotyped errors on addition due to their left-to-right tokenization. While performing addition, right-to-left tokenization shows drastic improvements compared to left-to-right tokenization (Singh & Strouse, 2024), but we cannot force models to do right-to-left tokenization just in the case of maths operations because, although right-to-left tokenization performs well on maths, it shows significant downsides while performing general tasks. This shows that LLMs mathematical performance strictly depends on how we present the numbers to them.

• Missing the reasoning and steps: When it comes to complex maths problems like algebra or calculus, these models solely rely on their training data correlations. Based on its training data, it tries to mimic the training data examples to solve the input question, skipping reasoning and skipping systematically going through steps. This probably leads to making errors while performing complex mathematical operations. Technically the model doesn’t have a “rough sheet” to reason out and work around the problem, since transformers are mapping the entire input to an output in one-go.

• No concepts for numeric precision: when it comes to numeric precision, LLMs don’t have any representation or concepts to deal with numbers, unlike software that uses 32-bit /64-bit floating or integer precision. It’s basic understanding about numbers comes purely from the training data. For example, the LLM might have learnt the square root of the number 2 is approximately 1.414 but it cannot derive its remaining digits in the floating points. This leads LLMs to make errors while performing arithmetic operations on high precision/large numbers.

• Training Data: Simply put, “Garbage in = Garbage out”. The training data might bring some bias to the trained model since the distribution of the mathematical content in the training data might be uneven; having a majority of simple math questions and very few complex math problems." Also, conceptually, the LLM training on the math data tends to cause the LLM to learn language patterns from math data rather than learning math problem-solving.

A few tricks to overcome these challenges:

• Chain‑of‑Thought Prompting: ask the model to show its intermediate steps before giving the final answer, increasing math accuracy by up to 40 percentage points on GSM8K with large models. arXiv
• Self‑Consistency (Majority Voting): sample many CoT traces and return the most common numeric result, typically adding another 4–12 pp of accuracy. arXiv
• Function / Tool Calling (ReAct, Toolformer): have the model emit structured JSON that triggers a calculator, database, or other API, then fold the result back into its answer. OpenAI PlatformMedium
• Program‑Aided Language Models (PAL / PoT): the LLM writes a short Python (or JS) snippet; a sandbox executes it and returns the exact answer, providing automatic verification. Acorn LabsHugging Face
• Full Code‑Execution Sandboxes: grant the model an internal “code interpreter” VM (e.g., ChatGPT’s Advanced Data Analysis) so it can iteratively refine and run scripts. Acorn Labs
• Specialized Math Engines / Agents: delegate heavy lifting to Wolfram | Alpha or similar, feeding precise symbolic or numeric results back to the chat thread. gpt.wolfram.comStephen Wolfram Writings

In conclusion

LLMs with Transformer architectures, despite their impressive abilities in natural language understanding, fundamentally struggle with math because they’re inherently designed to predict tokens rather than compute exact numeric operations. Their tokenization methods, lack of numerical precision, and the absence of explicit reasoning steps make them unreliable mathematicians, often getting close but not always exact.

References:

• Attention is All you Need; Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin, 2023
• Tokenization counts: the impact of tokenization on arithmetic in frontier LLMs; Aaditya K. Singh, DJ Strouse, 2024
• Testing GPT-3’s Mathematics Comprehension; I King